毎週土曜日の夜にブログを投稿していますが,このところ用事が立て込んできていることもあって,当面は週末から月曜日の朝までのどこかの時間に投稿することに変更します.おそらく日曜日の夜になることが多いと思いますが,とりあえず本日は今まで通り土曜日に投稿します.さて今日は何を書こうかと思案して,先ほどまで「Spearmanの順位相関係数」はどうやって出力するんだっけと,メニューを探っていたところでしたので,これを目指して書き始めます.
以前お話ししているかもしれませんが,今でもわたしの固有技術は計測だと思っています.新人当時は事業部として独立していた計測事業部に配属され,そこで産業分野における計測の重要性を勉強しました.技術分野としては陽のあたる存在ではありませんが,計測なしにはいかなる技術も立ち行かない,そう思っています.そのときからの計測技術に対する思い入れが今に続いています.初めてJMPを手にしたのも,自分がせっかく調整した計測装置のテータをユーザーに上手く使ってもらいたいということがそもそもの始まりでした.
サイエンスでも計測は重要です.数値化できなければそのいかなる対象もデータとして分析できないからです.技術分野では,製品ならばその性能,農産物であれば糖度や大きさなど,何を計測するのかは自明なことが多いので(精度や再現性という別の難しさがあるとはいえ)この点では工業計測は楽です.素直にその特性の計測値を「数値」とすれば良い工業計測と比較して,その一方で「数値」化が困難な対象もあるのがサイエンスにおける計測の面白さです.
例えば,社会科学や心理学のアンケート調査などでは,結果そのものは文字列であっても(すき・普通・嫌いなどのような)順序尺度の変数として数値化するのは容易ですが,研究目的を達成するためには上手いアンケートの作成が肝であるのはご存知との通りです.これは言葉を変えれば,計測手法を開発することに他なりません.抽象的な疲労や知性といった概念も状況は同じです.何らかの決まりに従って数値化可能ではありますが,そもそも何を計測対象とすべきかを研究者自らが決めなければなりません.例えば,疲労感VAS(Visual Analogue Scale)検査や知能テストが開発されています.
ちなみに簡単に説明すると, VAS検査では被験者に配られた検査用紙に「あなたが今感じている疲労感を,直線の左右端に示した感覚を参考に,直線上にXで示してください.」と指示されています.その下に描かれている線分の左端には「疲れを全く感じない最良の感覚」右端には「何もできないほど疲れきった最悪の感覚」とあって,その線分の上に自分でXを記入します.左端からXまでの長さを連続量として疲労度が数値化されるわけですが,再現性だとか個人の感覚の差だとかいろいろ計測技術としての問題は承知で採用されているわけです.そうでもしないと研究できないからです.
但し,疲労とか痛みという一般に認知されている概念を特定の(計測可能な)変数に紐付けるのには注意が必要です.VAS検査は世間一般に知られていないという意味で罪はありませんが,知能テストとなるとその対象となる知能の指標がIQとしてあまりに有名なのでいろいろと誤解を招きやすいのです.そもそも知能ということの定義が曖昧です.1904年にイギリスの心理学者Spearmanが一般知能の考え方を提案し,それを受けて翌年にBinetとSimonによって知能テストは開発されました.というわけでこの人が冒頭の「Spearmanの順位相関係数」 を提唱されたSpearman先生です.
知能テストは何を測定しているのか明確でなく,世間一般にはその結果指標であるIQだけが一人歩きしている状況だと思います.よくある誤解が,知能を知性と同じものと思うことです.検索すれば諸説出てくるはずですのでここには書きませんが,両者は明らかに違う概念です.仏教における知恵と智慧の違いにも似ているかもしれません.仏教では,知恵は煩悩の赴くままに使われるものであり,智慧は真実を見抜くために使われるものです.知恵はあるけど智慧はないという人がいることになります.知能と知性との違いがわかると,人口知能は人口知性ではないのだと納得がいくわけです.もちろん,IQと学歴との相関は明確に存在するので知性と何らかの関連はあるとは言えそうです.いろいろとある知能に対する考えの中で,もっとも納得がいくのが知能テストで評価されるものを知能と呼んでいるというものです.この知能を媒介して研究対象とする「現象」である知性などを代用計測していると考えれば腑に落ちます.
IQにはデータ分析のためだけでなく,社会的な意義もあります.例えば,知的障害者に交付される「愛の手帳」には1度から4度までの程度の区分があって,その認定にはIQが目安となります.東京都の場合で,最も重度な1度で概ね19以下です.これがどのような程度なのかは,IQはメディアンが100の正規分布であり,標準偏差は知能テストの種類によって異なりますが,15または16ということを知っていればわかります.従って,標準偏差を15とすると,IQが19というのはおおよそ5σと6σの間です.IQは工業計測における6σみたいなものだと考えればいいでしょうか.
このようにとにかく数値化することを第一優先とし,その数値が何を意味しているかはデータを取ってから判断するという計測もあるのです.こういタイプの計測はひとえに研究者の熱意とセンスの賜物です.わたしがいつも感心するのは生態観察研究におけるエソグラムです.対象とする動物の特定の行動(例えば求愛行動とか)に名前をつけることで,動物行動学で有名なローレンツ先生も研究のために飼っていた「ムクドリ」が興味を引いたものに対する嘴を開ける行動を「yawning (あくび)」と名付けています.観察対象のあらゆるタイプの行動を符号化したものがエソグラムです.エソグラムがあって始めて記録することができ,データ分析の対象となり得るのです.エソグラムを自分勝手に符合化しても意味はありません.そこには客観性が必要です.更に,数値化は分析の目的に応じてなされなければなりません.逆に分析の目的が定まらなければ数値化はできないということです.
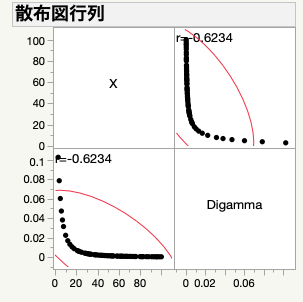
なんだかまとまりのない話になってしまいました.因みに.「Spearmanの順位相関係数」は分析メニューの「多変量>多変量の相関」の赤三角から「ノンパラメトリック相関係数」のサブメニューになっていました.このコマンドを実施するとこのようなレポートが表示されます.
これを見ればわかるように,単調増加の関数で作ったデータなのでちゃんと相関係数は1になってくれています.変数の挙動が不明であっても,単調増加(減少)くらいの制約であればおける場合が多いので,こういうときには有効な相関係数です.変数の数が非常に多くてJMPで多変量の相関のグラフを表示させるのが厳しいときなどは数値だけを見て判断せざるを得ないことがありますが,このときPearsonの相関係数では冒頭に提示したような非線形の相関関係は見逃してしまう可能性があります.こういうときでも,Spearmanの順位相関係数で引っ掛けることができるので,特に,量産データのように性質が不明であるような場合は,両方の相関係数でダブルチェックするようにしています.
来週はおそらく日曜日の更新になります.それではまた.


コメント