過去の投稿に画像リンク切れ多数ありご迷惑おかけしています．

COVID-19

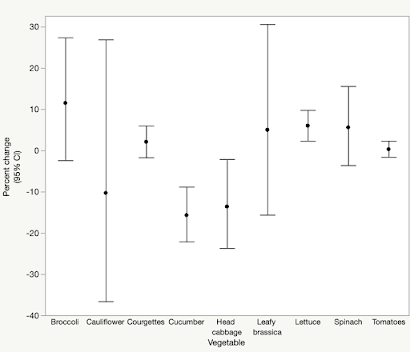
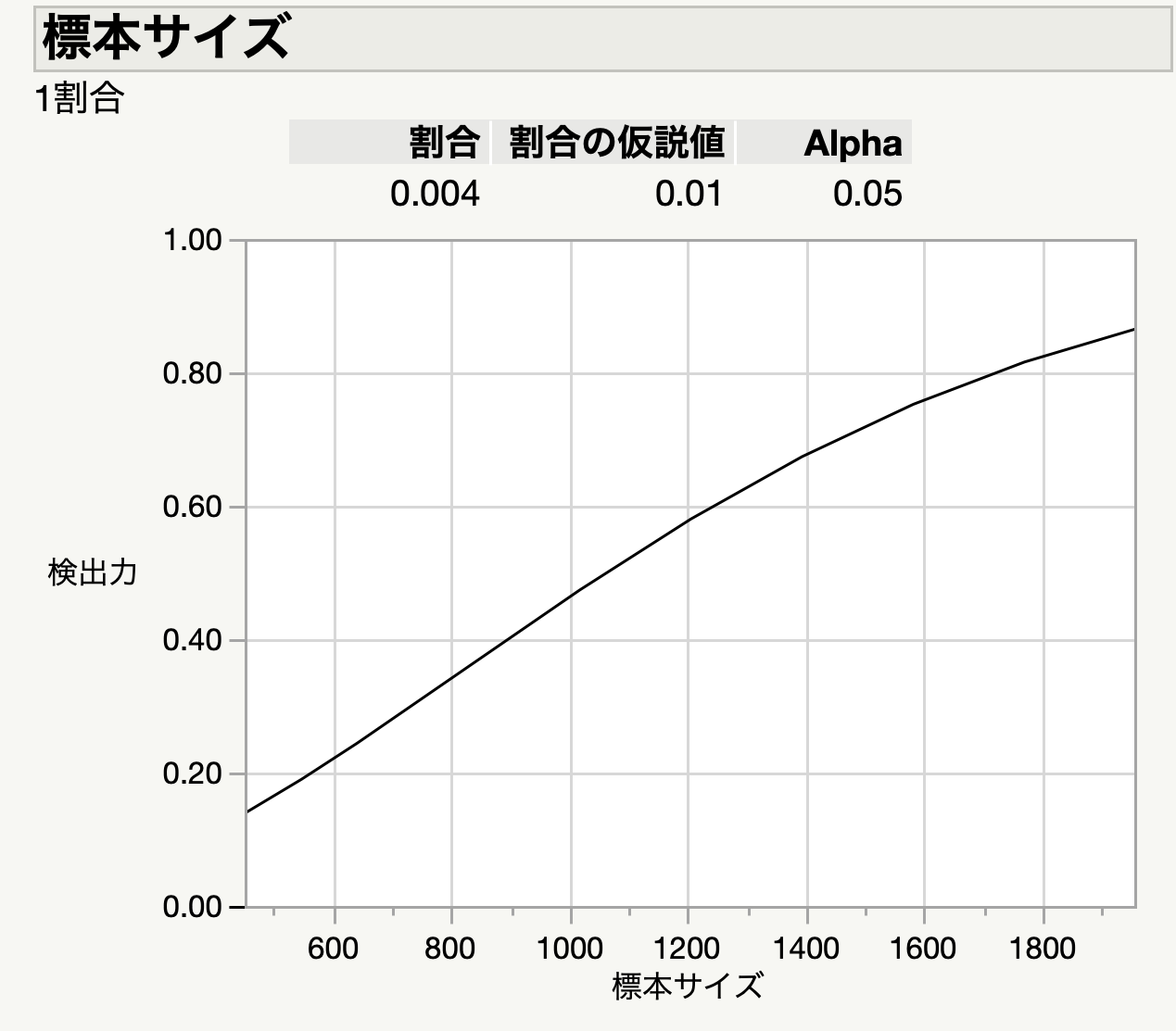
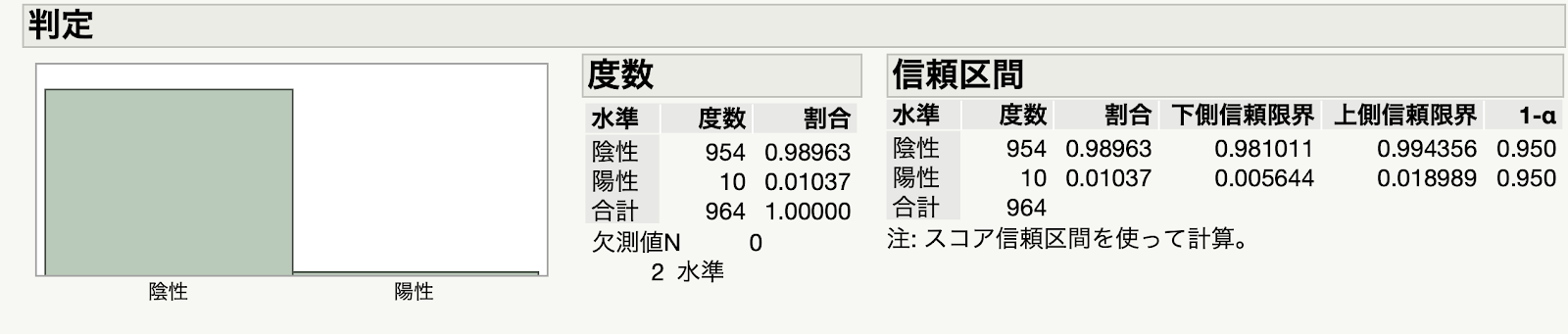
イベルメクチンと信頼区間

「イベルメクチン、新型コロナへの効果確認できず　国際チーム論文発表」という記事が出てました．イベルメクチンについては，データの改竄についてこのブログでも書いた記憶があります．このときから，既に証拠があやふやだと言われていたわけですけど，今回それがRCTによって証明されたことになります．new england journal of medicineに掲載された論文ということで，その影響力は水戸黄門の葵の御紋に匹敵します．何しろ，医学・生物分野での最高峰としてインパクト　ファクター75です．この論文誌に掲載される学者はそれだけで大変なエリートです．世界四大医学雑誌と言われているの...

トンでもな話

コロナでなにが残念かっていうと，日本人が分断されてしまったこと．これはいつかも書いた記憶があるけど，経済をまわせ派とロックダウン派だけでなく，マスクをする人しない人，最近ではワクチン派と反ワクチン派の分断なんかもある．ワクチンについては，反ワクチンの亜流の様子見派なんかもある．正直，気持ちの良いものではないですよね．こういうときこそ，正しい情報をもとにベストな判断をしなくてはならないのに，何が正しいのか何を信じれば良いのかはっきりしない．感染者のワクチン接種状況は治療に重要な情報だから，おそらく聞き取りしてると思うので，それを一緒に発表してくれてもいいのにと思います．既に感染者が何人...

ウイルスのパレートフロント

各地のコロナ感染者数が急増してます．デルタ株の感染力は従来の株の3倍弱というから，おそらくその蔓延が主要因だと思う．今までと同じようにしていては駄目なのに，今までと同じこともできなくなってきてたからね． CDCの報告のp15のグラフによれば，デルタ株の感染力は，1人が何人に感染させるかという，基本再生産量で5人から9人くらいだそうです．Chickenpoxは8人なので，同程度になってます．因みに，あちらでは水疱瘡のことをチキンポックスと呼びます．アメリカ滞在中にこの言葉は何度か聞きましたが，当時は子供が鶏からうつされる感染症だからかと勘違いしてました．語源は，特徴的な発疹が羽を毟った鶏...

jmp戦闘性？

東京のコロナ感染者数の発表は今日から1月3日までお休みなのだとか．HPに日々の数値は掲載されるそうだし，少しでも関係者の皆さんの負担を減らして，お正月くらいゆっくり休んで頂くのは良いことですよ．そもそも感染者数を毎日発表する必要もないと思うんだよね．そもそも感染状況の指標としては，感染者数よりも実効基本再生産数のほうが信頼できるし，その定義から変化はゆっくりになるので，いたずらに心配性の人がパニックを起こすこともないと思う．確かに，「COVID-19重症者におけるECMO装着数の推移」を見ても，現時点で日本全体で59件でそのうち９件が東京都だから，確かに感染は拡大している．実効基本再生産数と...

インフルエンザ様のこと

コロナ第三波と言われて久しいけど，なかなか歯止めがかからない．実効再生産数も１を切りそうで切らない日々ですね．それでも，東京に限れば，昨日は１を切ってます．またすぐに１を超えると思うけど．この繰り返しで，いわゆるテラスに載っている状況です．そんな中で，個人的にようやく感染拡大に歯止めがかかってきたとも思えるのは，「COVID-19重症者におけるECMO装着数の推移」を見て，なんと久しぶりに０人だったからです．0人は7月29日以来ですよ．もちろん，東京は0人になったとはいえ，全国では36人とまだまだ多い，でもピークは過ぎています．おそらく東京の感染状況が地方に伝搬するのに時差があるため...

ファクターXを探してみる

コロナ感染者増加で医療崩壊とか各方面で騒がれてるけど，誰かも言ってたように，崩壊という言葉は適切でないですよね．医療崩壊の定義が明確じゃないので，コロナ初期のイタリアのような状況（患者が廊下に放置されていたとか聞きます）になるののか，と誰もが思ってしまから．医療側の定義としては，そこまで破滅的なものではなくて，感染者が増大して医療サービスに大きな負荷がかかることで，その他の（通常の）医療サービスが提供できなくなることを医療崩壊と呼んでるみたいだけど．医療の負荷が増大するって言ってもインパクトが小さいから，医療崩壊という怪しい言葉を使ってるのかも．マーケティングにFUDっていうアンチ・...

アルコール消毒について考える

コロナが社会の仕組みにもたらした変化はいろいろある．リモートワークとかキャッシュレスへの半強制的移行とかが大きいところだけど，あまり関係ないという人もいる．リモートワークの普及は仕事の性質によるところも大きくて，営業さんがリモートワークってピンとこない．リモート営業なんて言葉も出てきたけど，実態はなにやってんだろ？知っている営業さんは，カタログの入った重い鞄を持って，一日のほとんどが移動だと言ってた．そのときはじめてパイロットケース（フライトケースとも）というものの存在を知ったっけ．対面コミュニケーションスキルも移動の手間もなくなれば，何をしたのかという実績だけがそこに残ります．これからは，...

統計リテラシー

先を読む話

まだまだ暑い日が続いていますが，いかがお過ごしでしょうか．いつになったら涼しくなるかと東京の10日間天気を見れば，まだしばらくは最高気温が30度以上で最低気温も25度以上の日が続くようでがっかりですね．実は，今年の夏は冷夏になるのではないかと，東北の古老が言っていたのです．7月に台風が一つも発生しなかったりして異常とは言われていましたが，過去の経験では，こういう年は不作に見舞われるのだそうです．気象庁の長期予報では猛暑であるとなってましたから，どうなることかと期待してました．古の知識が現代の科学技術を凌ぐというようなドラマチックな展開もあり得ただけに，科学的な予測に軍配が上がって内心ほっとして...

アオサとかキャベツとか

コロナ流行の初期に，感染防止に有効とされる食品がメディアに取り上げられました．覚えてますか？私の記憶によれば，納豆とかアオサとかがありました．アオサは某大学が公式に発表したものの，その研究のスポンサーがアオサのサプリを販売している会社だったことも問題視され，大学側が取り下げたはずです．一番問題だったのは，インフルエンザウィルスを使った実験結果でヒトコロナウィルスに対する増殖抑制効果を議論したことでしょうか．私のような素人でも乱暴と思いましたが，大学側の言い訳では，「ヒトコロナウィルスを含む各種ウィルスで効果があったから，新型コロナウィルスにも効くんじゃね．」としか言ってないのに，勝手に「新型コ...

コロナ時代のメディアリテラシー

最近の報道ではコロナ対策についての主張が二極化しています．以前から言われていた，コロナなんてただの風邪という意見と，現状の危機を認識しPCR検査を積極的に実施して，感染者を炙り出すことで，部分的にでもコミュニティをロックアウトせよという意見です．それに誘導されてでしょうか，私たちの間にもある意味対立が生じてしまっているのは残念なことです．二週間後には日本はどこどこの国のようになる・・・という従来からのマスコミの基調に乗せられている人々もいる一方で，渋谷ではクラスターフェスとかいうノーマスク，ノー自粛を標榜する団体の催しが開催されたりしています．そもそも，医療や政治あるいは経済の観点だけから最適...

統計リテラシー

また抗体検査の話

一段と世の中が騒がしくなってきましたね．そんな中で菅，今日もブログだけは平常運転でいってみたいと思います．そうはいっても，特に書くこともないので，先週に引き続き，時事ネタを強引にJMPと紐付けてるという恒例のチャレンジをしてみます．先週は，横須賀市のコロナ抗体検査の結果の解釈に，統計的でもないのに「統計的に」という枕詞をつけるなと文句を言いました．そもそも「統計的に」という言葉をつける言説には，騙されるなという警告の意味があると解釈しています．さて，最近は，様々な自治体で同じ試みが実施されているようです．数日前のニュースでは宇都宮市でも無症状者を対象に抗体検査を実施したようです． ...

JMP統計学覚え書き

統計リテラシーと抗体検査

今日読んだニュースによれば（今日のニュースではありませんけど），インテルが７nm半導体の技術開発が予定より６カ月遅れていることを明らかにしたことで，株価が１割近く下がりました．Mac搭載のCPUとして毎日お世話になっていますけど，つい先日もAppleがCPUをインテル製から内製へと移行していく方針が発表されたばかりです．自社の製品開発のロードマップを他社の開発の遅れに妨げられないようにすることが目的と言われています．おそらく，インテルも今後は外部への生産委託を拡大する方向へ舵を取っていくことになると思いますが，同じ業界に長いこといて，かつての同僚のアメリカ人なども働いているので他人事のようには...

JMPJMPではじめるデータサイエンス統計学覚え書き

次のページ

12