書籍サポート
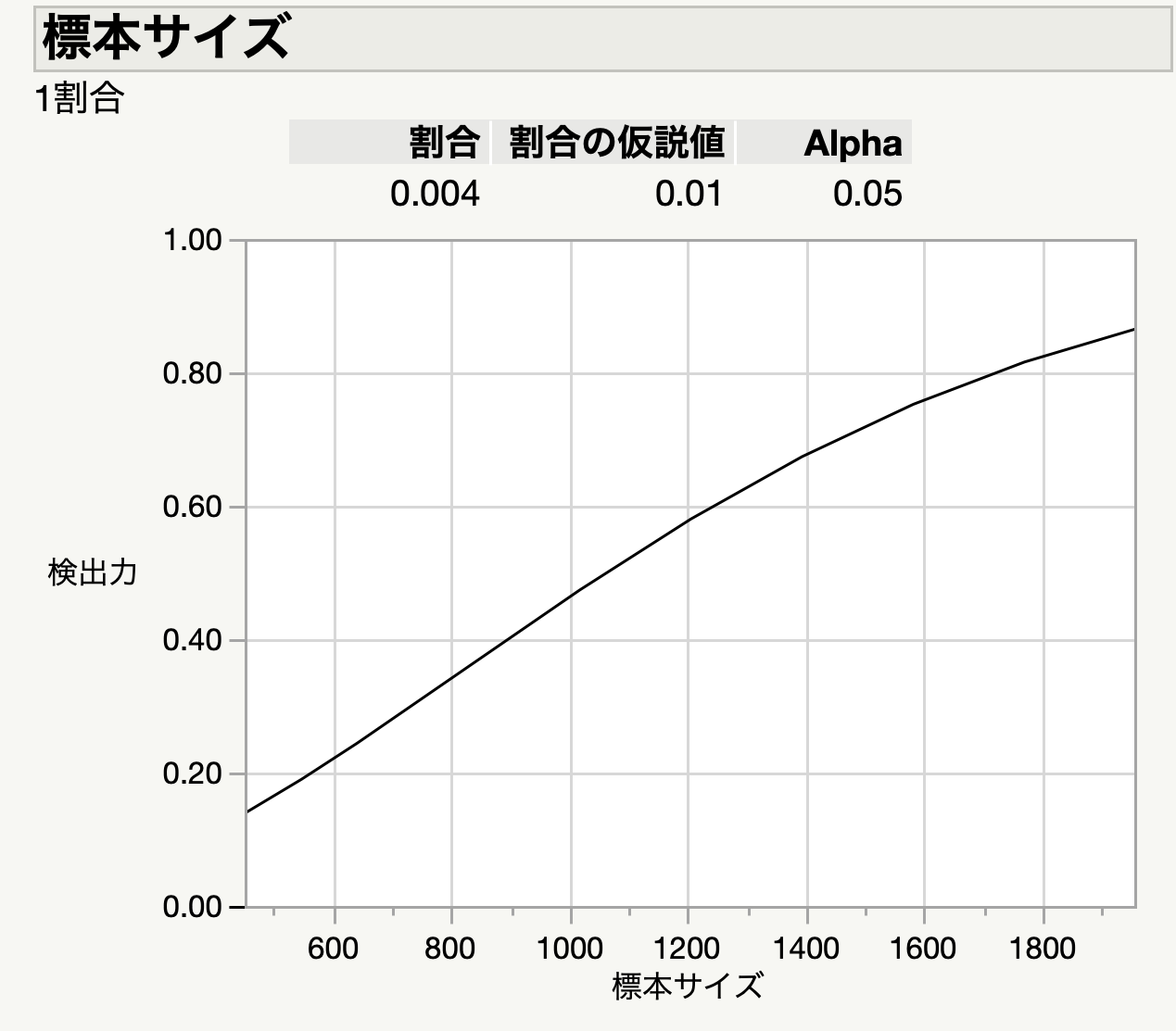
書籍サポート問1の解説
『統計学のやさしい授業』は本日発売になりました.まだここにおいでになる読者の方はいないと思うけど,今後しばらくの間,本書に掲載した練習問題の解説をしていこうと思います.JMPユーザーの方には申し訳ないです.あ,ちなみにJMPというのはSAS社の統計ソフトです.詳しくはこちら.ご存知ない方は値段が気になると思うけど,個人で購入する人はまずいないと思います.サブスクだしね.AdobeのCreative Cloudの数倍はします. JMPをご存知ない人は,無料で使えるPythonとかRとかあるのになんで統計ソフトにお金を払うの?と思うかもしれないけど,まあその価値があるから六本木に立派なオフ...