今日読んだニュースによれば(今日のニュースではありませんけど),インテルが7nm半導体の技術開発が予定より6カ月遅れていることを明らかにしたことで,株価が1割近く下がりました.Mac搭載のCPUとして毎日お世話になっていますけど,つい先日もAppleがCPUをインテル製から内製へと移行していく方針が発表されたばかりです.自社の製品開発のロードマップを他社の開発の遅れに妨げられないようにすることが目的と言われています.おそらく,インテルも今後は外部への生産委託を拡大する方向へ舵を取っていくことになると思いますが,同じ業界に長いこといて,かつての同僚のアメリカ人なども働いているので他人事のようには思えません.
その巧の技を阻害するものの一つが分業化です.ですから,同じ会社組織に臆していてもそこに十分なコミュニケーションが図られていなければ意味がありません.インテルでも設計と製造とが分業化してしまい,同じ会社であってもデータの受け渡し程度の関係になっているのかもしれません.このことは,他の会社組織を見ても想像に難くないです.もちろん,分業化には経営効率の観点からは多大なメリットもあるので,いかに部門間のコミュニケーションをとっていくかが巧の技にとって大切になります.そのベースになるのが統計学であり,それ以前の統計リテラシーと考えています.これについは,そのうち書きます.
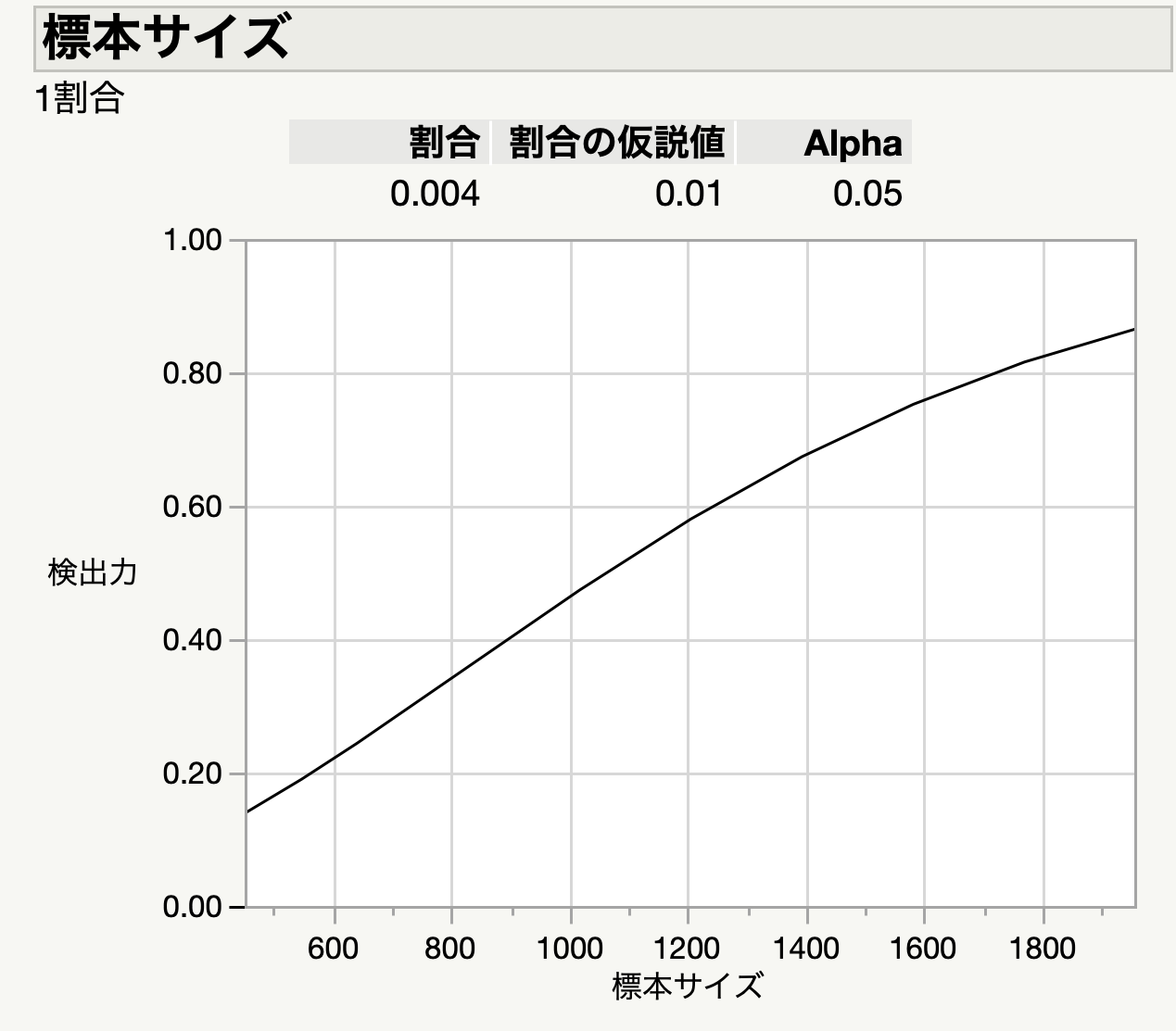
というわけで,近頃は統計リテラシーの講座なんかをいろいろ開いているのですが,今回のコロナ騒動で多くのネタが拾えるので,その整理に追われている毎日です.例えば,治療薬として期待されている「アビガン」の臨床研究についての藤田医科大学の報告が報道されました.明確な有効性は確認できなかった,即ち有意性なしとの結果について,サンプルサイズを大きくすれば有効性が出てくるかもしれないとのことです.まだ,実際の報告を読んでいないので,メディアの報道だけから判断するのは危険ですが,『JMPではじめるデータサイエンス』の読者の方であれば,事前に検定力をもとにサンプルサイズを決めてるべきであることお分かりと思います.望み通りの結果が得られないからといってサンプルサイズを増やすのは,特に今回のように人命に関わる重要な研究では口に出すのさえ憚られることです.間違った検定で間違った判断を下すことの影響ははかり知れません.研究チームには統計の専門家もいるはずなので,おそらくメディアの誤解によるものと思ってますが,正直驚きました.この件については,後日検証してみたいと思っています.
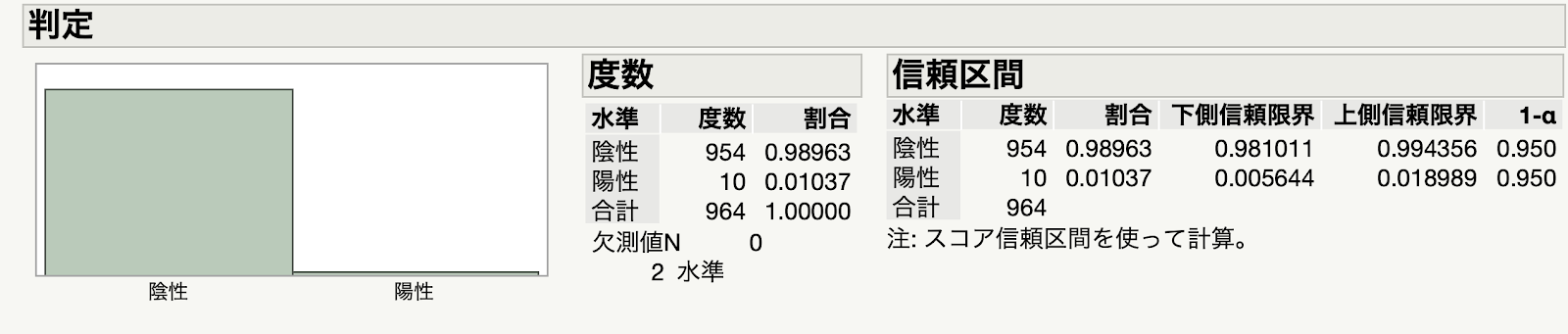
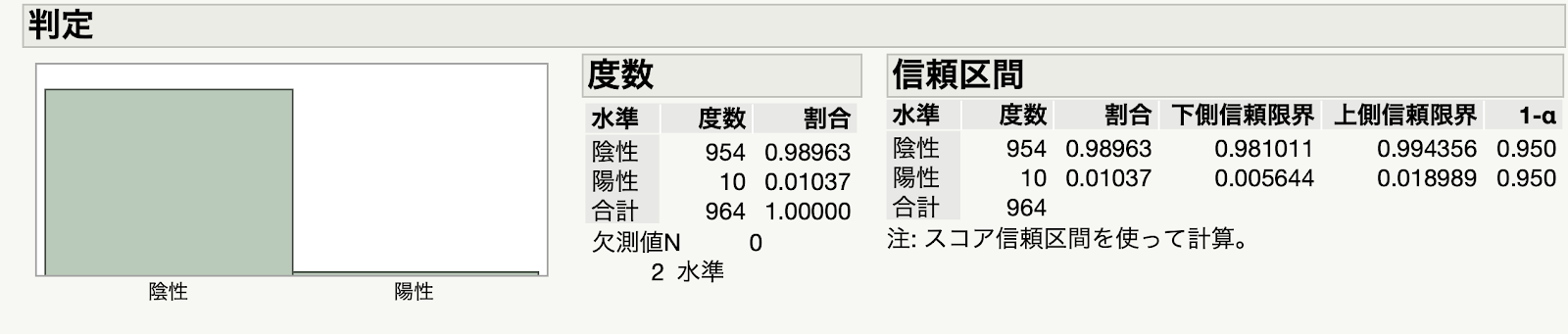
他の報道でも,首を捻ることがありました.横須賀市が無作為に抽出した市民の抗体検査をしたのですが,その結果を受けて,市長が「人口に比例させれば、4000人が感染したことがあるということになり、非常に高い数字だと受け止めている。自分も感染している可能性があるという意識を持って行動をとってもらいたい。」と発言しています.自分も感染している可能性があるという意識を持って行動するのはもちろん,その通りですが,統計リテラシーでこの結果を捉えると,いくつかの問題が見えてきます.
因みに,この信頼度を99%にすれば信頼区間は1833人から8869人となりますし,更に,10人のうち半分が偽陽性だとすると,下側は677人になります.非常に多いと判断するのではなく,こんなもんだくらいに受け止めればいいのでしょうが,このために440万円かける価値があるのかは検討すべきですね.

通常の統計ソフトならば,nやpが小さいときは,ウィルソンの信頼区間を使うということを知っている必要があるますが,JMPだとそこを良きに計らってくれます.とはいえ,これが正規分布の母比率の信頼区間とは違うことを知らなければ,計算結果が異なることに戸惑います.そこで注が書いてあるわけです.英語版では「conputed using score intervals」と書かれているので直訳です.日本のユーザーには,スコア信頼区間ではなくウィルソンの信頼区間とした方が親切だと思うのですが,いかがでしょう.他にもWelchのt検定なんかも,統計学を前提としない間口の広さはJMPらしいですが,日本語の教科書で勉強した人には不親切ですね.その割には,「Fit Y by X」が「二変量の関係」と妙にこなれた日本語になっていたりするのが不思議なところです.聞いたところでは,芳賀先生がそのように命名されたとも聞いていいます.変な用語もありますが,まあJMPは外人だと思って付き合っていくのがいいのでしょうね.
それではまた.

コメント