(記事は掲載時の環境(移転元)で書いてます.ここは移転先のブログなのですけど,文言は修正してませんのでお間違えなきよう.)
いきなりなんですが,近日中にこのブログを移転します.いろいろ事情があって前から計画してたんですけど,面倒なのでつい今になってしまいました.今月で今のサーバー(以前のブログがあった場所)の年間契約が切れるので,ついに重い腰をあげたという次第.ここはBloggerなのでサーバーがどこにあろうとも関係ないけど,このブログは移転先で続けます.今月中は更新しますけど,来月からはこちらでの更新は停止する予定です.以前のブログはすでに更新を止めて久しいのですが,あちらは以前のブログの記事と一緒にサーバーごと消えます.大したこと書いてないので,それでもいいかと思ったのだけど,一応こちら(Blogger)にコピペしておきました.リンクは確認してないし,Bloggerの仕様で一部の表示も崩れてます.画像もうまくリンクしてないかも.過去記事を読まれる方はそんなに多くないと思うのですけど,その点はご勘弁を.
それで,ブログも移転先で続けることにしました.今度のサーバーではWord Pressが使えるのですが,やっぱり楽ですね.この機会にブログも趣向を変えようかと考えてます.テンプレートに「お問い合わせ」があるので,それを使ってみます.時々いただいていた質問にも,よりセキュアにかつ素早く対応できるんじゃないかな.記事カテゴリーもいつもだんだんごちゃごちゃしてしまうので,今度こそよく考えてみます.おそらく更新のタイミングなども変わるかもしれません.毎週日曜日に書いているのですけど,仕事が不定期になるので決まった時間を取るのが困難になりつつあります.記事も,できるだけJMPには拘っていたのですけど,もっと気楽にかける内容にして続けていければなとも思ってます.「JMP超入門」なんてコロナ自粛期間中に,読者を意識した記事を書こうと意気込んだりましたけど,どうもそれだと長続きしない.ブログの原点に立ち戻ります.
SNSはFaceBookとTwitterのアカウントを持ってますけど,どちらも休眠状態です.自分でいうのも変だけど,若山牧水タイプな人間なんで,どうもああいうのは苦手なのかも.あ,Linkedinは勧められて最近アカウント取りました.仕事繋がりもあって,面白いですね.20年ぶりの友人とも連絡取れました.アカウントお持ちの方は,よろしかったら「つながり」を申請してください.まだ繋がっている人が少ないので寂しくないと言っては嘘になります.若山牧水じゃないのかよ,というツッコミが聞こえてきますが,そもそも人間嫌いではないのですよ.むしろ教えたがりのところもある.だから遠慮しないで,新ブログでは「お問い合わせ」してみてください.
それで,今週からブログの原点に立ち戻って,今何をしているか書きます.訳あって,また書籍執筆してます.それが今度は統計の本なので,ある程度マイルールを打ち出せるJMP本とは勝手が違っていろいろ悩んでます.そのうち,まとめて書こうかと思うけど,今の悩みが不偏標準偏差のところ.ご存知のように不偏標準偏差は不偏分散の平方根ではないのだけれど,エクセルの定義がそうなっているからか,そのように書いてある教科書もあったりします.おそらく著者の頭では,不偏分散の平方根を不偏標準偏差と定義しましたよ,ということになっていて,普遍性(期待値が母数になるよ)のことは忘れているのでしょうね.でも,その場合でも,不偏分散の平方根は不偏推定量ではないということを教えなくちゃならないと思うんですよ.
エクセルは統計ソフトじゃないから,許されるのかもしれないけど(影響を考えるとそうとも言えないかも),実はJMPでさえ,同じ状況なのです.意外と知られていないことだけど,「一変量の分布」の「要約統計量」レポートにデフォルトで表示されている「標準偏差」も不偏分散の平方根なんです.エクセルのように不偏標準偏差としていないから間違いではないけど,多くの人がこの「標準偏差」を標本標準偏差と思っているんじゃないかな.それで,どのくらいこの値と母標準偏差の推定値が異なるのかと思ってJMPの「要約統計量のカスタマイズ」を探したら「不偏標準偏差」が見つからないんですね.「ロバスト標準偏差」というM推定の統計量はあるんですが,ないんです.JMPなら,ここには「不偏標準偏差」のチェックボックスがあって欲しかった.本当にないのか確認しておきますけど,とりあえず電卓代わりにスクリプトで計算してみました.

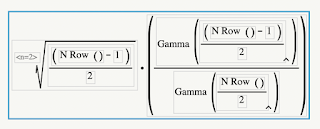
おそらくこの計算式でいいと思うのだけど,間違いあればご指摘ください.コピペで検証できるようにテキストでも書いときます.
Root( (N Row() – 1) / 2 ) * (Gamma( (N Row() – 1) / 2 ) / Gamma( N Row() / 2 ))
不偏分散の平方根にこの係数をかけたものが不偏標準偏差になるはずです.サンプルサイズ10だと1.02810925326662 になります.実はこんなことしなくても近似式があるので,ちょっと検算してみます.Root((n-1)/(n-1.5))を計算して,こちらは1.02899151086ですか.まあまあいい近似ですね.サンプルサイズが100ならほぼ1になります.大きな違いはないので目くじら立てる必要はないと思いますけど,本当はそれは正しくないということを読者に伝えるべきかが悩みなのです.
オプションは次の三つです.
1.世の中間違っている(こともある)ことを正しく伝える.エクセルの不偏標準偏差は不偏推定量じゃないぞ.
2.実務的に違いはないので,多くに倣って不偏分散の平方根とする.
3.薮蛇になるので,標本標準偏差には触れない.
1で行きたいところだけど,初心者向けの本でガンマ関数なんて無理.そもそも中学数学の範囲でって言われてるし.2は一番幸せなのかもしれないけど,自分としては嫌だなと思う.3しかないのかもしれないけど,迷ってます.皆さんはどう思われます?
それではまた.

コメント