MCDAアドインについてのお知らせ

MCDAアドインを使うには，ノイズ因子をモデルに取り込む必要があるので，それが難しいかもしれません．因子数が多い場合は，当然ながら実験数の圧縮のためにカスタム計画を推奨します．とはいえ，数因子程度であれば，まずはカスタム計画で「RSM」でモデルを作れば十分です．具体的には，p248の「やってみよう」をマスターしてください．（今，手元には第二刷しかないので，それ以外の刷ではもしかしたらページ数が異なっているかもしれません．）サポートファイルは「虫の目.jmp」を使えば，計画を作成する手間も省けますよ．ここから，P254までの正味6ページをしっかりフォローできれば，MCDAアドインの免許皆伝です．背後にある考え方については，本文中でも書いてありますが，そのうちもう少しわかりやすく解説します．

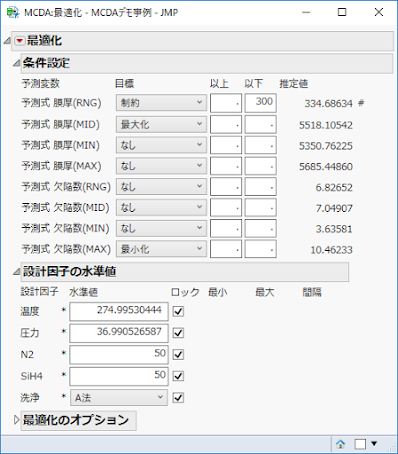
ここで重要なことを一つリマインドします．本文中にも書いてありますが，自分のJMPで得られた結果と本書の図版の最適化の結果とは，JMPのバージョンやOSの種類，CPUの種類，その他様々な環境の違いで，必ずしも同じになりません．だから，本書で示した結果は参考にとどめ，異なる結果が得られてもそんなものだと思ってください．重要なのは，満足度関数の小数点以下の違いがあるだけで，どちらも最適化の候補だということです．例えば，私の環境（WIN10，i7，JMP15.0）ではp265のJMPくんの解は，このような結果となりました．

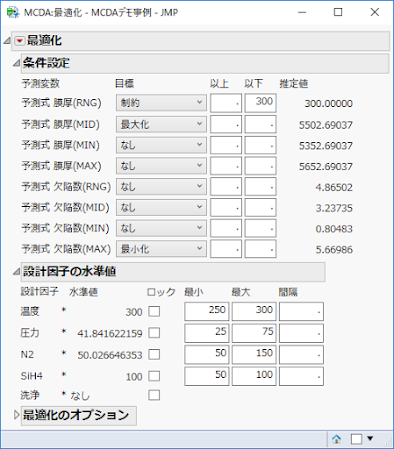
 この本を執筆する際は，SAS社の方で図版を作成してもらったので第一刷では，その環境での結果が掲載されています．その後，MCDAアドインの改良で計算結果に違いが生じたので，第二刷ではその当時の自分の環境での結果に差し替えました．今回の結果は，それらとも違っています．この例題のように予測式が二つもあって．ノイズ因子も二つあるような複雑な統計モデルに対しては，PCによる最適化で得られるのは，所詮は近似解なのでこれが実態です．この例題をつくったとき，複雑にしすぎたとは思ったのですが．応用編ではできるだけ実践的な状況を再現すべきと考え，敢えてこのままにしました．このため，初心者の方が不審に思われるかもしれません．

このような解の不安定性を解消するため一つの方策が「最適化のオプション」のパラメータを変更することです．シード値以外を5倍程度を目安にして変更すると本文にも書きました．ですが，実践的には解を追い込むという手順を推奨します．例えば，上の解ではN2が50.026646353となっていますが，最適解としてこれが受け入れられるのであれば，「ロック」にチェックを入れて50を入力します．その上でもう一度最適化します．そうすれば，N2＝50という制約下での最適解が得られることになりますね．さらに制約を加えていくことで最終的に所望の最適解に到達するという手順です．この手順では真の最適解にはなりませんが，そこそこ近い最適解が得られる過程で，何がボトルネックになっているのかなどの情報も理解できるようになります．

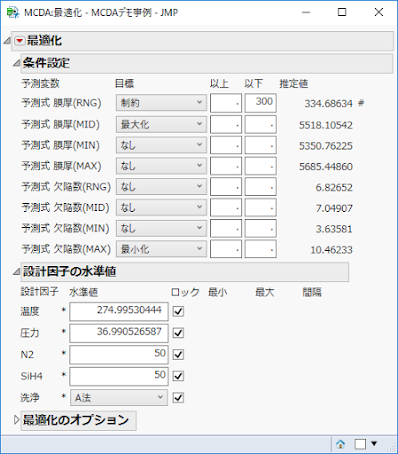
因みに，冒頭に全ての因子をロックして書籍掲載の最適化を入力した結果を示しました．そうすると得られた最適値も書籍とぴったり一致していることがわかります．この最適解の揺らぎは，MCDAのバグではなく，最適解の不安定性によるものだということがお分かりいただけると思います．

この手順に加えて，「条件設定」も変更していくのが常套手段です．このときJMPだけでは実施不可能な（スクリプトを作れば可能です）範囲の制約を条件にできます．このアドインの価値はこれだけではありませんので，ぜひ自分のデータで試してみてください．質問等はこのブログのコメントでいつでも受け付けています．非公開になっているので，遠慮なくどうぞ．『データサイエンス』の方でももちろん構いませんよ．会社からですとコメント欄が表示されないこともあるらしいので，その場合はご自宅からお願いします．

それでは，また．