リモートワーク中に拙著で勉強して頂いた方が多くいらしたようで,ありがたいことです.最初にリリースしたのが『統計的問題解決入門』だったので,こちらを先に購入してくださった方も多いのようなのですが,JMPの基本操作を勉強するには少し不親切だったかもしれません.もう一度書きますが『統計的問題解決入門』は実験計画で,『データサイエンス』はデータ分析を学ぶのを目的としています.ですので,JMP初心者が最初にお読み頂くならば『データサイエンス』をお勧めします.実験計画,特にJMPでは標準的なカスタム計画に興味がある,あるいは実務で使いたいという方は『統計的問題解決入門』をどうぞ.書名が親切でなかったために,逆の順番で読まれている方がいらしゃるのであれば申し訳ないです.言い訳をすると2冊も書くとは思ってなかったので,シリーズを意識した書名をつけることができませんでした.
実は,更にもう一冊書くという話もあるので,今から書名を考えているんですが,ビジネス書ではないので,出来るだけ単純明快にすべきと今から肝に銘じています.最近は,高級食パン屋で「迷わずゾッコン」とか「パンのペリカン」「考えた人すごいわ」「だきしめタイ」「なま剛力スタジアム」「生とサザンと完熟ボディ」「うん間違いないっ!」「もはや最高傑作」などなど,変な名前の店名が流行っているそうです.他店との差別化が狙いとのことで,何でもほとんど一人のプロデューサーが名付けているそうです.書名を考えるときにも,やはり他書との差別化や検索にかかりやすさなどは考慮します.
本書も『JMPではじめるデータ分析』が仮題だったように記憶してます.書名を決めるにあたり,「データ分析」で検索するとエクセル系のビジネス書が多く出てくるから,それらと差別化しようというオーム社の意見で,候補の一つとして出していた『データサイエンス』になったという経緯があります.いつかもブログに書いた記憶があるのですが,多くの人がデータサイエンス= 機械学習と思っているので,私自身はデータサイエンスという言葉に躊躇いがありました.もっと高度なことを期待されていた方ががっかりされるかもしれないことを恐れていたわけです.本書はデータサイエンスとタイトルにつけましたが,初めてJMPを触る人のための操作入門にもなるように,実践的「ハンズオン」として読んで頂くことを想定して書きました.
最近,質問を頂いたのですが,その割には逆に少し難しい部分を端折りすぎたかなとも思っています.そこで,本日は改めて『JMPではじめるデータサイエンス』のP238の練習31について補足します.この問題は,実際にカスタム計画のサンプルデータ「カスタム計画.jmp」を使って,「モデルの当てはめ」の練習をするという趣向になっています.天下り式にサポートファイルを開くところから始めても良かったのですが,それだけでは,実験計画がこんなにも簡単に作成できることが伝わらないと考え,敢えてカスタム計画の作成手順を示しました.裏の話をあかすと,当初,実験計画について1日割く予定にしていたのですが,ページ数の制約から断念しました.その名残が問題31と問題49及び問題50なのです.本当はこの三つの問題で一つの節を構成していました.
本書のカバーする範囲を超えてしまったのですが,「モデルのあてはめ」や「満足度の最大化」の練習と割り切ればよかろうと考えました.とはいえ,初めて実験計画を知った方には,こりゃなんだい?となったかもしれません.日常的に実験計画に関わっているものにとっては何でもないことですけど,それらが唐突に出てくるので不思議に思われたようです.『統計的問題解決入門』の方にはカスタム計画の作成を詳細に書きましたが,わざわざ購入して頂くのも申し訳ないので,少々補足します.
練習31で扱っている事例の背景は,p239の下の方に書いてあるように,宮川雅巳(2000)『品質を獲得する技術』日科技連に掲載されている品質工学の事例がもとになっています.この書籍にはデータが掲載されているのですが,残念ながら製造条件は書かれていません.品質工学では,設計因子を質的に扱うのでこれは当たり前なのですが,このような場合でも,設計因子の上下限をそれぞれ1と-1にすることでモデリングしてそれを元に最適化することが可能です.P238の設定ウィンドウで,宮川(2000)で値が与えられている「水分率」「発泡剤」以外の「値」が-1と1になっているのはこのことが理由です.
この連続尺度化する,即ち名義尺度を連続尺度として扱うのは統計的問題解決ではとても重要なテクニックです.量的因子は連続尺度で扱うのが鉄則と肝に銘じてくださいね.更に,具体的な値が分かっていればそれを使うのも重要です.宮川(2000)からは以下のように読み取れます.
発泡剤: M1→3.9,M2→4.3,M3→4.7(単位:PHR)
水分率: 低水分率→0.52,高水分率→0.81(単位:%)
応答の「発泡率」の「下側限界」「上側限界」がそれぞれ20,30になっているのも宮川(2000)でそのようになっていたというだけの理由なので,このことを説明してなければ,カスタム計画の何かの設定なのかもと真面目に捉えてしまうのももっともです.特にこの問題では「実験の回数」が「発泡率」下限と同じ20であることも紛らわしかったですね.カスタム計画で得られたデータは問題31でモデル作成に使われ,更にこのモデルは,この後の問題49と問題50とでパラメータ設計で最適解を得るために使われます.ですから,最後まで進んで頂くともう少し見通しが開けると思います.
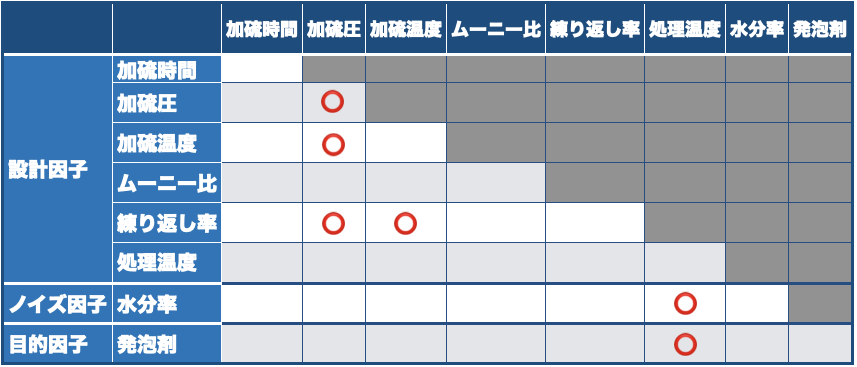
「モデル」に入力する効果も天下り式なので補足しておきます.発泡ゴムの製造工程はこの図のように可塑化と架橋化の工程に分かれていて,それぞれは独立である(交互作用は小さい)と見なせることがポイントです.

細かい説明は割愛しますが,そのことを踏まえて,この事例では以下の固有技術の知見を仮定しています.
1.発砲率に影響する因子は8
2.加硫圧,加硫温度,練り返し率の影響が大きい
3.上記の因子間に交互作用があると予想できる
4.発泡剤,水分率は処理温度との間にのみ交互作用がある
5.加硫圧には非線形性があるかもしれない
それを元に冒頭に掲げたようなテーブルを作成します.『統計的問題解決入門』ではこのテーブルを使って具体的にカスタム計画を作成する方法を紹介しているのでよろしければ参考にしてください.ある程度これらの情報を知っていることが前提になりますが,カスタム計画ではこれらを使うことで実験数を削減できるのです.
技術よりの機能でもあり,JMPの入門書としてはカスタム計画はその理論を理解するにはやや難しい面もありますが,本書でその威力に邂逅する人がいればいいなと思いました.強引だったかもしれませんが,不明なことあれば遠慮なくお問い合わせください.注意として,最近判明したのですが,どうやら一部の会社からは書き込みができないようです.どうやらセキュリティポリシーの問題のようですが,何も返事なければご自宅から再度ご連絡いただければありがたいです.Bloggerに引っ越して結構経つんですが,ここも色々使いにくいところ出てきたのでまた引越しを考えているんですが,なかなか時間が取れません.
それではまた.


コメント