5月,6月と開催されていたJMP On Airも今週で終了となりました.コロナ期間中は自宅で楽しみながら勉強させていただきました.あらためてSAS社の皆様にお礼をしたいと思います.第一回の開催ではまだオンライン視聴に慣れていなかったということもあって,少しドキドキしてスタートを待ったのは良い思い出です.1時間もヘッドセットをつけているのは辛いので,スピーカーから音を出しても邪魔にならない場所に移動して視聴していたのですが,当初は自宅の通信状態が安定せず,時々音声が途切れがちになったりして苦労しました.自宅のWifiは5GHzと2.4GHzを使い分けているのですが,調べるとその切り替えが物理的な場所によってうまくいっていないことが判明しました.幸い,その部屋には有線LANを壁に埋め込んでいたので,それを使うことができました.電気屋さんにCD管だけ埋め込んでもらって,自分で配線を引き回したのですが,当時は既に無線LANの時代でしたから,こんな手間をかける価値があるのかは悩みましたけど.実際,ほとんど使っていなかったのですが,まさかWifiの速度が有線を抜くような時代になって,有線が活躍するとは思っても見ませんでした.
実際使ってみると,間違いなく早いし何よりも安定しているのは,今後オンライン授業をする立場としては心強く,少なくとも私の環境では有線は適者生存をしていくようです.ポストコロナ時代には変化に対応できないものは淘汰されるという趣旨のことを,(実際には言ってもいない)ダーウィンの言葉として引用した政治家がいました.変化に対応するという能動的な能力よりも,偶然を受け入れることができたという,どちらかといえば受動的な能力が,その種が生き残るには重要なんではないかと思っています.哲学的に色々難しいことを言う先生もいらっしゃいますが,要するに,運が良かったからに過ぎないのではないかと.その偶然を受け入れることで,たまたま適者となって生き延びたと言う例がたくさんあります.体色が白い蛾が,ヨーロッパにおける工業の発展に伴って発生した公害の影響で黒っぽくなっていったという現象を工業暗化といいます.19世紀後半に観察されたこの現象は,どの生物学の教科書にも載っているほど有名ですが,最近,と言っても2006年ですが,その原因が究明されました.Hof, A., Campagne, P., Rigden, D. et al. The industrial melanism mutation in British peppered moths is a transposable element. Nature 534, 102–105 (2016) によれば,ゲノム上の位置を転移するので動く遺伝子と言われるトランスポゾンの挿入が工業暗化の正体であることが突き止められました.それを変化する能力と考えることもできますが,一般的には偶発的な現象の結果として暗化した個体が発生し,それがたまたま公害で黒くなった樹木が保護色となって生き残ったのだと考えてもいいと思います.
偶然を受け入れる能力が自分に備わっているかということを,ポストコロナ時代(未だ渦中ではありますが)の今考えています.適者生存というよりは運の良いやつが生き残る時代です.どうすれば良いのかを統計思考で考えると,試行(trial)と揺らぎが重要なのはのではないでしょうか.運はある程度制御できます.それにはとにかく試行回数を大きくし,試行を繰り返す度に行動に小さな変化を取り入れるのです.このテーマは古今東西,各所で取り上げられてます.古くは星新一のショート・ショートにもあったような記憶がありますし,手塚治虫の『ザ・クレーター』にもこのテーマの短編が収録されています.1993年のアメリカ映画『Groundhog Day』もそうでした.(今調べたら邦題は『恋はデジャ・ブ』なんてひどいのが付いてたんですね.)
ポストコロナでは,日常でも変わったなと気づくことが多々あります.近所に深夜まで営業している割と有名な食堂があります.お客さんが10人も入らないくらい小さいお店なんですが,最近外から覗いたらその狭い店舗になんと間仕切りを設置して営業していました.その光景を見るととてもシュールです.お店に入るときに体温を計測する(される)ところも多くなったということですし,自分自身も仕事で人前でお話しするときに,非接触型の計器で体温をチェックされたりします.咳と発熱が特有な症状という感染症ですから,最も簡単な検査法ではあるのですが,信頼性はいかほどのものなんでしょうか?正常域の上限を37度あるいは37.5度としているところが多いと思います.前者は水銀体温計のデザインから,後者は法律による定義なのですけど,実はともに科学的な根拠はありません.調べれば,日本人の平均が36.89±0.34度という値があちこちに書かれています.これは田坂定孝,日新医学 44(12), 635-638, 1957が参照されているのですが,ここに示されているRangeは1σです.だから結構多くの人が上限の37.23度を超えます.このデータは古いので,現代の人の実態を反映しているのかも不明です.少なくとも老人性低体温症というのがあるくらいですから,年齢によっても基準が違うはずですし,ホルモンの日内周期の影響も受けるはずです.そもそも分布は正規分布なのかと思ってpubmedを漁ってみたら,こんな論文がありました.Myroslava Protsiv, et al, eLife 2020;9:e49555 DOI: 10.7554/eLife.49555
アメリカ人のデータですけど,この157年の間に体温が下がり続けているということとともに,Figure 1—figure supplement 1に分布が示されています.これによると,正規分布というよりは自然災害のリスク計算に用いられる極値分布のような裾が非対称な形状をしています.一般形は一般化極値分布(generalized extreme value distribution),属に GEVなどと呼ばれますが,体温の分布はその特殊系のガンベル型です.ガンベル分布などとも呼ばれますけど,ガンベル先生は私たちのよく知っているフィッシャー先生と一緒に極値理論を展開されたことで有名です.極値理論はリスク工学と密接に関係していて,エイヤでいうと,分布の裾の挙動に重きを置く統計理論です.乱暴ですが,平均よりも最大値を標本の代表値に据えていると言ってもいいかもしれません.リスク工学,例えば大風による被害や,河川の氾濫などの自然災害系の統計解析をされる方には馴染み深い分布かもしれません.
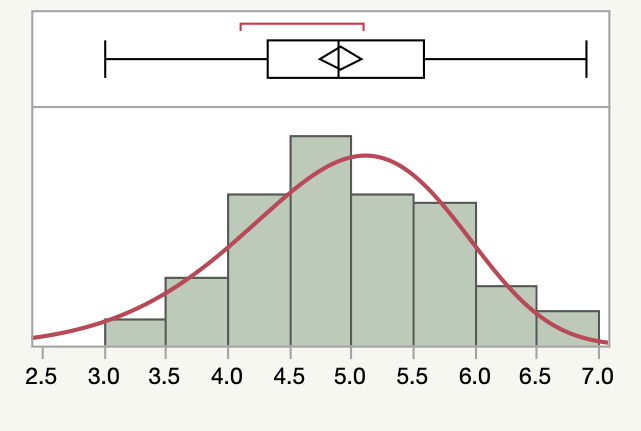
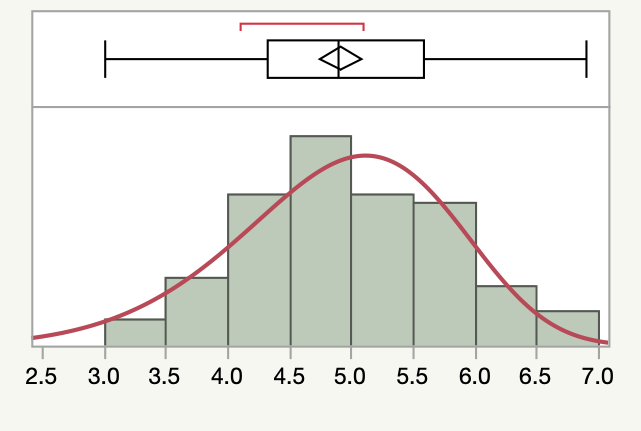
JMPでは極値分布は「一変量の分布」プラットフォームに出てきます.冒頭の図は,「Iris.jmp」の「花弁の長さ」に対して「種類」の「setosa」を抜いたヒストグラムに「連続分布のあてはめ>極値」を適応したものです.因みにJMP15ではUIが少し違います.低値側の裾が少し厚くなっているのがお分かりでしょうか. この様子は箱ひげ図に赤い線で示された最頻区間と平均との関係を見てもよくわかりますね.もう一つJMPで極値分布を目にするのが「生存時間(パラメトリック)のあてはめ」プラットフォームです.因みに,分析メニューの「信頼性/生存時間分析」の下にあります.設定パネルの『分布』のところに「最小極値」と「最大極値」とがあって「対数正規」や「Weibull」の代わりに使ったりします.そういえば,信頼性分析でよく使われるWeibull分布も極値分布の一つですね.因みに,JSLでは,SEV Density(x, mu, sigma)関数が実装されています.
私の関係する事例ではあまり極値分布が出てこないので,実際の事例に使ったことはありませんが,平均を代表値とする手法に限界を感じることが多くなってきたいので,極値理論に興味はあります.ポストコロナでは,適者生存のために今までとは違ったアプローチを取り入れていきたいので,少し勉強してみようかな.
それでは.



コメント