前々回の記事で,プロファイルの「誤差因子」に何らかの因子を割り当てると,等高線プロファイルに尾根線が描画されるというtipsを紹介しました.こうすることで,割り当てた因子の微分係数が特性に加わり,それにゼロ望目の制約を加えることで,その因子をノイズ因子としたロバスト設計が可能となります.本書にダウンロード添付したMCDAアドインはロバスト(パラメータ)設計のためのアドインですが,プロファイルでロバスト設計ができるのに,なぜ,このようなアドインが必要なのかという質問をいただきましたので,今週はそれにお答えします.
短い答えを言うならば,何をしてロバスト最適とするのかという定義が違うというのが一つの理由です.少し丁寧に説明すると,プロファイルにおいて,満足度の最大化で得られるのは誤差因子に対する応答関数の微分係数を0にする解です.例えば,次のような応答関数を考えてみると状況が良くわかります.因みにこの応答関数はサポートファイルの「ロバストデモ.jmp」から作ったものなので皆様もお試しください.ご覧のようにこの応答関数は二山あって,∂X=0の制約を課して満足度を最大化したのが次の図です.
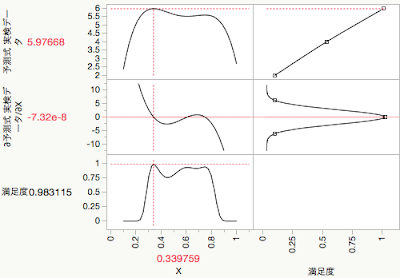
∂X=0の点は3つあるわけですが,ここでは特性値に最大化の制約をかけているので,左側の山の頂点が解として導出されます.因みに,最大化の制約を外しても,その上でトリップの数などの「最大化のオプション」を増やしても(デフォルトでは20ですが,例えばそれを100とする)安定して左側の山が解となります.JMPの満足度最大化の癖のようなものでしょう.他のオプションを変更して試行錯誤すれば,左側の山の頂点以外が出てくるかもしれません.もちろん,特性を最小化にすれば真ん中の谷がこのように検出されます
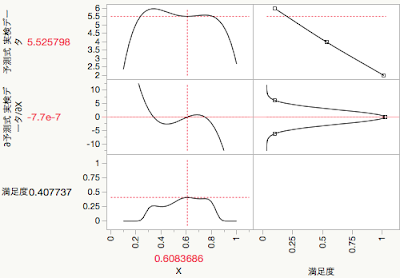
しかしながら,一般的な工業分野でより重要なのは右側の山の頂点(付近)です.特性値の変動という点では右側の頂点にある方がより大きなXの変化を受け止めやすいからです.この解は,微分係数に制約をかけることだけでは得られません.このためには,ロバスト化の指標を(特性の変動の)範囲(Range)においた最適化が有効です.但し,この場合でも状況によっては右側の山の頂点は出てきません.
下に示した解は,Xの変動を5%とした場合に導出したロバスト解の例です.(このような単純な例ではMCDAアドインは適用が難しいので,この例ではHOPEアドインを用いています.)ここに示したように,特性の制約次第で色々なロバスト解を暴くことができます.


この暴くというフィーリングが特に工業分野での最適化では大事です.最適解は1つではなく,それは周囲の状況(社会情勢,時代)やステークホルダーにより刻一刻と変わって行くからです.ですから最適解そのものよりもシステムが内包している最適解の可能性を暴くことにより深い「意味」があるのです.その「意味」をシステムのオブジェクトと捉えれば最適解の候補がインスタンスということになります.
何よりも多目的最適化においては可能な限りロバスト化の制約は緩めておいたほうが都合が良いのです.ユーザーはロバストだからという理由で製品を購入はしないからです.一般的に,微分係数を0とするのはかなり強い制約です.この制約に引き摺られて特性の真の最適解を見逃す危険があります.ロバスト化の制約を緩くして,ばらつきは所望の範囲に入ればOKというケースがより好ましい場合がほとんどです.もちろん,微分係数に範囲の制約をかけることでも構いませんが,想像するのも困難なので通常は数値指定はできません.
このような範囲によるロバスト化を実現するのが本書に付属したMCDAアドインやHOPEアドインなのです.両者の違いについては以前お話ししたかもしれませんが,重要なことなので回を改めて説明したいと思います.因みに,来週のDiscovery Summit Japan 2018に参加される方は,そこでMCDAアドインの応用例の発表がありますので,ぜひお聞きになってください.
それではまた.


コメント