先週に続いて今週も執筆での悩み事などを書いてみます.今回の書籍では『統計的問題解決入門』よりも初心者を対象にしていますが,その線引きに悩んでいます.先週も検定をどこまで深く学んでいくかの線引きに悩んでいると書きましたが,例えば,「Box-Cox Y変換」を取り上げるべきかどうかで今は悩んでいます.
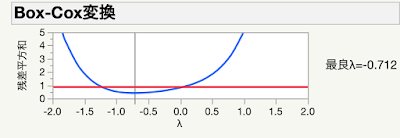
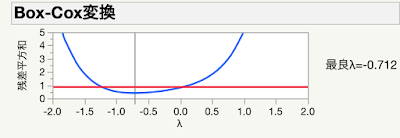
最良λで目的変数を変換して,正規分布に近づけるという強引さに躊躇うものがあって,最近まで気に留めていなかった手法なのです.先日,最良λではなく(信頼区間内で)半端が出ないλを設定するのでも良いとわかって,少し見方が変わりました.例えば,信頼区間内に0があればλ=0(即ち無変換)とすることが妥当と判断できることになります.もう少し深く勉強しようと,原著論文の G. E. P. Box and D. R. Cox (1964), Journal of the Royal Statistical Society. Series B, Vol. 26, No. 2, pp. 211-252 を読んでいるのですが,さすがに統計学の論文で手強いです.
このJRSSは論文の最後にDiscussion on Paper by Professor Box and Professor Coxと題して,他の統計学者によるおそらく座談会のようなもの?が掲載されているのが面白いですね.その冒頭はあの実験計画でも有名なNelder先生です.「オックスフォード(辞書)のBox and Coxで定義から始めてもよろしいでしょうか.」などと言っているので不思議に思って調べたら,確かに辞書にBox and Coxというのがあって,イギリスの喜劇から取られた慣用句で二人一役という意味らしいです.それに続き,あのTukey先生の言葉を引来つつ,データ分析における二つの問題を指摘しています.
一つはデータに異常値(rogue observations)がないことを確認する方法とそれがあった場合のアクションであり,もう一つはモデルが正しいものであるかを確認する方法です.その上で,後者の手法としてこの論文で提案されたBox Cox変換を捉え,ベイズ統計の観点から議論されています.続いて,やはりベイズ統計のHartiganの必要十分条件で有名なHartigan先生のコメント,更に待ち行列で有名なKendall先生がTurkey先生の文章を読み上げたりしています.Plackett-Burman計画で有名なPlackett先生も文章で登場したりして,本当にそうそうたるメンバーばかりです.やはりイギリスは統計学では先進国なんだと実感します.もっとも,Coxはロンドン大学ですが Boxはアメリカのウィスコンシン大学ですけれど.
というような文献を読んでいて今日も時間がなくなってきました.とはいえ,この論文を読んでその精神が理解できたので,ページ数の制限にかからなければ掲載しようと決めました.ベイズ的な考え方を身につけるにも良い手法と思います.とはいえ.少し高度な内容であることも事実なので,読者に「ここは飛ばしてもいいよ」ということを知らせる工夫が必要かもしれません.これを書いていて,項目ごとにEasy,Normal,Hard(ゲームみたいですけど)をマークするというアイデアを思いつきました.
これからその作業に取り掛かりますので,本日はこれにて.


コメント