全国的なコロナ流行の影響で運動会を中止にする小学校も出ているそうです.運動会は嫌いな子もいるけど,悲しがってる子もいるだろう.高校だけど,私の母校は運動会が盛んでそれこそ1年のメインイベントだったので,その気持ちは痛いほどわかります.
「棒倒し」とか「100人ラグビー」とか色々と変わった種目があって,その練習は放課後はもちろん,昼休みもやるのですよ.そうなるとお昼ご飯を食べることができないので,当然早弁と言って休憩時間にに弁当を食べるわけです.それもクラス全員が.今にして思えば,バンカラな校風だったですね.共学だったけど,女子も早弁をしていたのが印象に残っています.
運動会を中止するのは密になるからということだけど,これはとても日本的だと思っている.蜜という言葉はその反対の粗と付になって,粗密(疎密)という言葉として使われることがほとんどなのです.海外ではソーシャル・ディスタンスというけど,こちらが連続変数なのに対して,密は質的変数の水準と考えてもいいかもしれない.
もちろん,日本でもソーシャル・ディスタンスはあります.一応2mということにはなってるけど,ほとんどの場合,密を避けるで済ませているように思います.日本的だと思うのは,暗黙の了解が確立しているから,アメリカのソーシャル・ディスタンスが1.8mなのは,6ftにしたからだろう.あの人たちmってほんとわかんないです.因みに,フランス人とかイタリア人のような濃厚接触民族だと1mになってます.
質的変数は量的変数よりも情報が少ないので,その少ない情報で規律正しく行動できるのは素晴らしいと思う反面で,情報が少ないことに慣れてしまって,私たちの行動が雑になってないかとも危惧してます.日本て紋切り型の政策が多いからね.これは私たちが思考停止になっていることに責任もあるのだけど.
例えば,このグラフは『JMPではじめるデータサイエンス』のp82に掲載した図だけど,年齢を連続尺度にすることで,9歳から12歳にかけての男女での平均身長の逆転現象が観察できます.
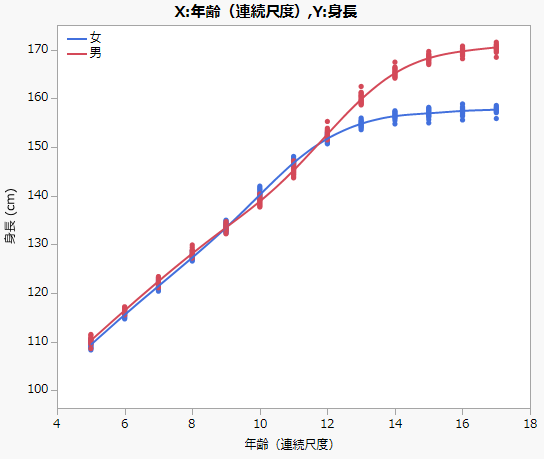
この現象は質的変数の棒グラフにしても観察できるし,グラフビルダーでは名義尺度でも「平滑線」を描かせることはできます.だけど,目的変数と説明変数を共に量的変数にして関係性を見るのが基本です.年齢のようにどちらの尺度でも考えられる変数では,連続尺度とすることで情報の抜け落ちが防げ,より詳細な関係性を見たり,それを元にした判断が可能となります.
密になるからといって,運動会を中止する根拠にも量的な関係性を取り入れて,もっと細かく行動のON,OFFを切り替えていくべき.流行当初はデータがなかったから,密になると感染する(しやすくなる)といった雑な行動規制でも良かった.だけど,もう1年以上も経つんだから,距離を**にすると感染リスクが**低減する,といった量的なデータを元にきめ細かく(即ち量的に)行動するように誘導して欲しいですね.
今日は時間がないので,ここまで.



コメント