目黒のさんま

書籍サポート

11.17.202001.26.2020

先週お知らせしたように，『統計的問題解決入門』にバンドルしたMCDAアドインの最新版を明日（来週の月曜日）からリリースします．機能的には変わりはありませんが，JMP15に対応して使用期限も1年延長されています．JMP15をお使いの方は最新版のダウンロードをお願いいたします．先週言及した不具合は解消されているのですが，一つ注意したいことがあるので本日はそれを解説します．

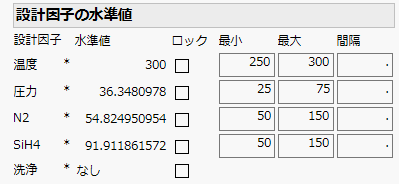
P257からはじまる「MCDAアドインによる意思決定」の例題のような比較的複雑な状況では，新バージョンでは書籍に掲載した最適解とは異なります．ここまで応答関数が複雑な場合は，通常あまりないとは思いますが，以前と異なる結果が出るかもしれないことをご了承ください．この理由については，p258の「この例題についての注意」に書いた通りです．「満足度の最大化」のロジックはヒューリスティックなので，初期値などの各種設定によって必ずしも同じ最適解が得られるとは限らないのです．このことは本質的に避けられません．最初は気持ち悪いかもしれませんが，いずれそ，統計モデリングによるパラメータ設計では最適化は推定値であり，最適解はそもそも信頼区間により提示されるべきものだと理解できれば素直に受け入れることができます．もちろん，実務では最適解は一つに定めなければならないので，この例題のように大きな不安定性が懸念される場合は，p260の説明にあるように「最適化のオプション」の設定を変更してみてください．

このように，最適解の不安定性はシミュレーションの丸め誤差に由来するわけですが，システムの本質に根ざしている場合もあります．初期値の変動が結果を大きく変えてしまう「バタフライ効果」を特徴とするカオス系のシステムが知られています．ここで言う「バタフライ効果」とは，もともとは気象分野での数値予報に起源を持つ表現です．「ブラジルで一頭の蝶々が羽ばたけば，テキサスで竜巻が起こる」などと象徴的に語られることが多いのですが，初期値に対して鋭敏なシステムの予測不能性を意味しています．

日常でもサイコロを振って出る目の数は現時点ではどんなに高性能なコンピュータを使っても予測できません．わずかな初期値の変動がどの目となるかを決定してしまうので，高精度なサイコロを使っても結果は予測不能です．因みに，一部の人には有名な「世界最速のサイコロ」なんてのがあります．最速というのはタイポではなくてF1のエンジンに使われている金属と同じだからとか聞きましたが，マーケティングがうまいですね．このサイコロを振ってもその結果が正確に予測できるわけではないです．あくまでも大数の法則に従った経験的確率が数学的確率と一致すると言うことです．

モデルや最適化の条件が複雑な場合，初期値に対するシステムの最適解の鋭敏性は大きくなります．ですから，モデルを不必要に複雑にすることは多重共線性だけでなく，最適解の不安定性も招きやすくなるのです．モデルをシンプルにするには，「効果の要約」レポートで「R2乗」を見据えつつ「対数価値」を参照して「要因」を『削除』していけばいいのですが，あまりシンプルにしてしまうと技術的に面白みがなくなってしまいます．「目黒のさんま」と言う落語がありますが，モデルの複雑性を不安定性をもたらす厄介なものと捉えるか，それともシステムの旨味と捉えるかが技術者次第というところでしょうか．

もう一つ付け加えておくと，最適化の条件を複雑にしても解は不安定になりやすいです．とはいえ，設計画面で条件を変更するのは簡単ですから，この場合は最初は単純な条件を置いて，次第に複雑にしていくと言う原則を守ると良いでしょう．具体的には，まず単特性で最適化します．ロバスト設計の場合であっても，このときY（MID）かY（RNG）のみに条件を入れることがポイントです．その上で，制約条件を入れていきます．最初は広くそれから狭くしてみてください．この過程で解の不安定性に遭遇することもあるかもしれません．MCDAアドインによる最適化はこの過程により得られる多数の最適解を踏まえて，技術者が勘と経験，固有技術の知見を加味して統合的に決めることになります．

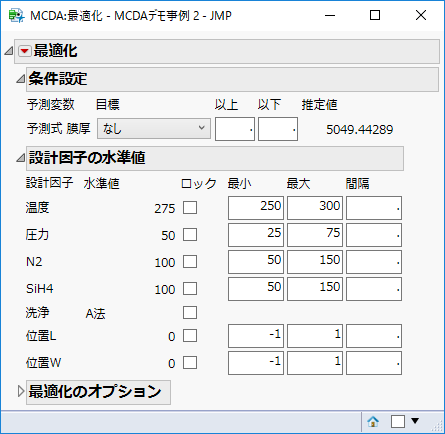
ということで，最新版のMCDAアドインによる最適化の結果は書籍掲載のものと異なる場合もあることをご了承ください．因みに私の環境では，p259の結果は冒頭の図に示したようになります．p260，p261下，p262の結果もついでに示しておきます．