ここのところブログ投稿する時間が取れなかったけれど,そろそろ落ち着いてきた感じです.願わくば.といっても今日も小ネタですいません.前回,二項分布の正規近似の問題について解説しましたが,それについての補足をします.
打ち合わせのときなどに,確率の概算をパッと提示できると格好いいのですけど,二項分布の計算は暗算ではほぼ不可能なので,正規分布に近似する必要があります.このとき,前回お話したように,成功ー失敗条件を満たしていることを確認することを忘れないようにしてください.ところが,この条件を満たしていても,近似がうまくいかない場合があります.
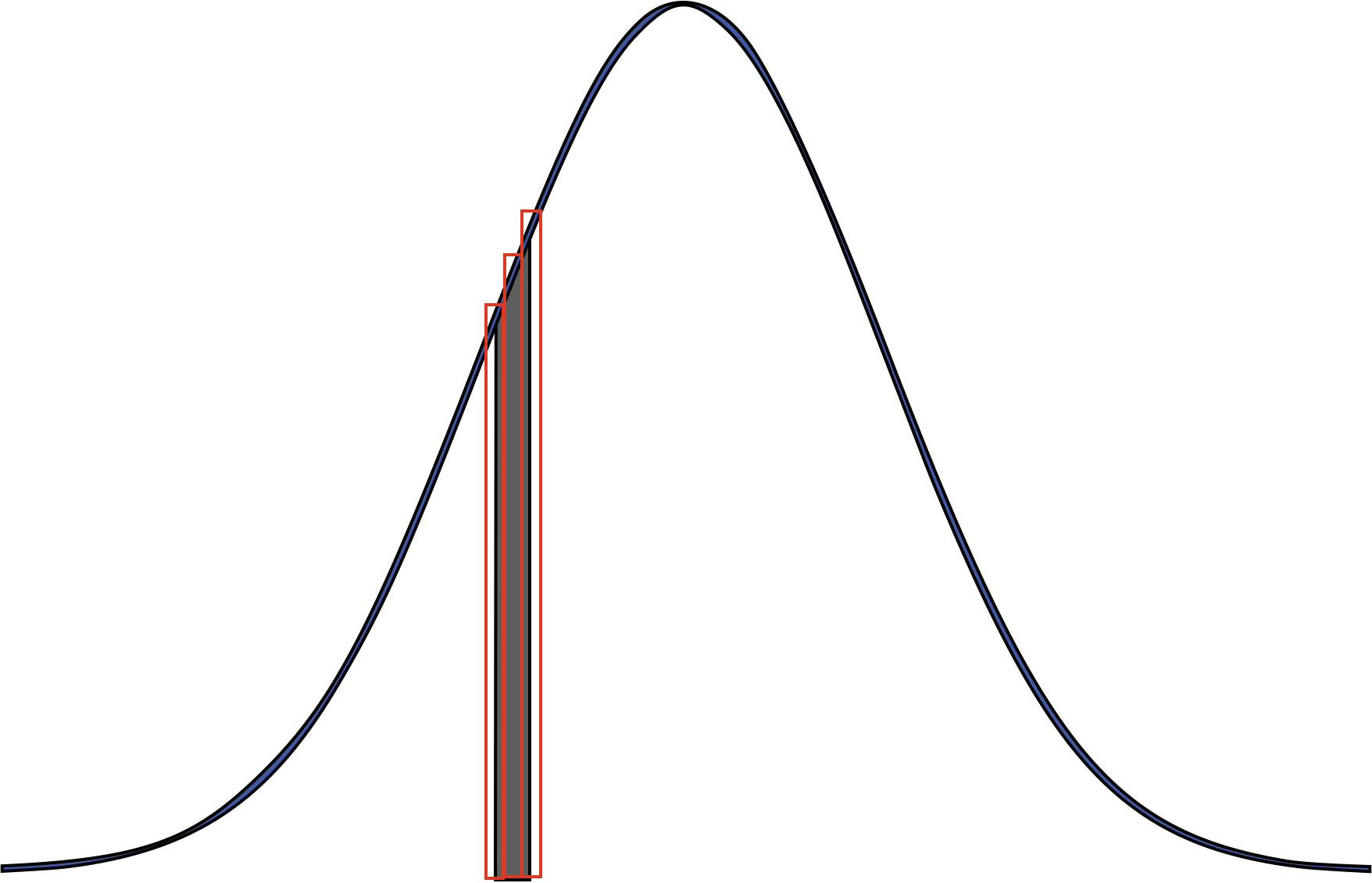
どういう場合かというと,確率変数の区間幅が狭い場合の二項分布の正規近似では,近似誤差が大きくなります.この状況は,二項分布は離散的であることに由来します.下の図をご覧になれば理由はお分かりいただけるでしょう.
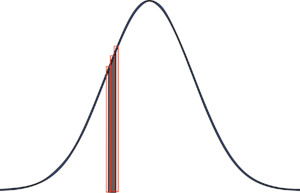
こういうときは,領域の下端値を0.5減少し,上端値を0.5増加すると,精度が向上します.この補正を連続性補正(0.5補正)と呼びます.特に区間幅が小さいときはこの補正は必須です.
統計学にはいろいろなところで近似が出てきます.中心極限定理もその一つ.近似であるならば,限定した条件のもとで成立するのだということを忘れないようにしてください.
それでは.


コメント