本日は先週の続きです.「パターンを調べる」を使ってデータ捏造の痕跡を調べることができたけど,その際,設定項目の「値」のことろに「先頭文字と末尾文字」というのがあるのに気付いた.これは,もしかしたらデータがBenfordの法則に従っていることを調査できるのかと思ったら,ビンゴでした.
Benfordはアメリカの物理学者で,彼が見つけた数値データの先頭の数字の出現頻度についての法則はBenfordの法則と呼ばれてます.データがべき乗則に従うという前提はあるけれど,たいていの実測データでは,先頭の数字の出現頻度は1が最大で,数字が大きくなるに従って低下していくというもの.
それによれば1の相対出現頻度はおよそ0.3で,8がおそよ0.05なので,この値を覚えておくといいです.因みに,この法則を等比数列に対して証明するのは意外と簡単です.
例えば2の等比数列を考えます.先頭が1となる条件は次のような不等式で表せます.
$$1×10^m\leq2^k\leq 2×10^m$$
ここでmは任意の整数ですね.
$$\frac{m}{log2}\leq k\leq \frac{m+log2}{log2}$$
と変形できるから,$k$の区間幅は
$$ \frac{m+log2}{log2}-\frac{m}{log2}=1 $$と計算できます.$m$が消えちゃうところが味噌ですね.
同じようにして,先頭が2の区間幅を計算すると,$\frac{log3 – log2}{log2}$となることが示せます.最終的にすべての先頭数字の区間幅を足し合わせると$\frac{1}{log2}$となるので,先頭の数字が1になる相対頻度は$log2$となります.即ち,おそよ0.3ですね.
計算の過程を追うとよくわかるんだけど,$log2$の2は2のべき乗に由来するのでなくて,先頭数字を$n$と一般化すると$log(1+\frac{1}{n})$となって,$n$だけに依存することが示せます.
それで,先週の捏造があるとされたイベルメクチンの臨床データにBenfordの法則を適用してみました.コロナに対する重症度の指標はいろいろあって,最近では(その後の消毒作業などに)手間のかかる胸部CTに代わって,血液検査で代用することが一般的になってます.
重症化の指標にもいろいろありますが,このデータテーブルには変数名に「serum ferritin」があって,しかも実験前後の値が記録されてます.血清フェリチンは鉄を貯蔵するたんぱく質で,基準値は男性20~250ng/ml,女性10~80ng/mlのところ,コロナ重症の目安は430ng/ml以上のようです.コロナ感染で活性化したマクロファージから分泌された炎症性サイトカインが,異常高値の機序と考えられてます.
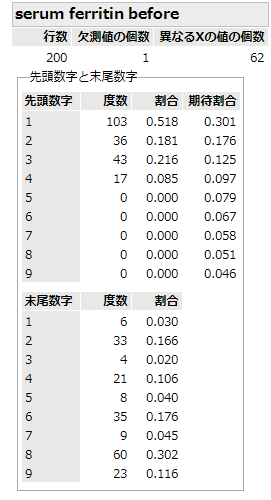
さて,捏造するなら実験群だろうとの考えから,イベルメクチンの投与前後のフェリチンの観測値の先頭数字を調べてみました.投与前のデータでは,数字が大きくなるにつれ度数が減るという傾向は見られます.少し1の出現が多すぎるようで,少し極端かなという感じはしますが.
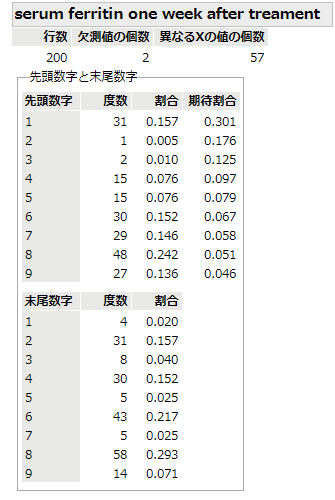
一方,イベルメクチン投与一週間後のデータでは,明らかにBenfordの法則からの逸脱がある.何しろ,先頭数字が8が最頻度数ですよ.Benfordの法則の理論値を使ってカイ二乗検定にかけてみるまでもなく,統計学的には明らかに不自然です.捏造がなければ,あり得ないほど珍しいデータということ.
一般に,人が数値を捏造するときは,ランダムを意識するあまり,先頭数字の出現頻度が均等になる傾向があるのです.このデータは全てが捏造でないようなので,判断は難しいところだけど,少なくとも「怪しい」というフラグを立てることはできそうかな.
JMPでは末尾数字も出力してくれるのですが,これは何に使えるのかもう少し考えてみます.
それでは.


コメント